Leetcode 3: Finding Longest Substring without Repeating Characters

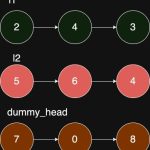
Problem Description

Given a string s, find the length of the longest substring without repeating characters.

Example 1:

Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

Example 2:

Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3:

Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.

Constraints:

• 0 <= s.length <= 5 * 10^4
• s consists of English letters, digits, symbols, and spaces.

Approaches

Approach 1: Brute Force

Algorithm:

1. Iterate through each character in the string as the starting point.
2. For each starting point, extend the substring while checking for duplicates.
3. Keep track of the maximum length of substrings found.

Time Complexity: (O(n^3))
Space Complexity: (O(min(n, m))) where (m) is the character set size.

Python Code:

def lengthOfLongestSubstring(s: str) -> int:
    def all_unique(substring):
        return len(substring) == len(set(substring))

    n = len(s)
    max_len = 0

    for i in range(n):
        for j in range(i + 1, n + 1):
            if all_unique(s[i:j]):
                max_len = max(max_len, j - i)

    return max_len

Approach 2: Sliding Window

Algorithm:

1. Use two pointers to represent the current window.
2. Move the right pointer to expand the window until a duplicate character is found.
3. Move the left pointer to shrink the window until the duplicate character is removed.
4. Keep track of the maximum length of substrings found.

Time Complexity: (O(n))
Space Complexity: (O(min(n, m)))

Python Code:

def lengthOfLongestSubstring(s: str) -> int:
    n = len(s)
    char_set = set()
    left = 0
    max_len = 0

    for right in range(n):
        while s[right] in char_set:
            char_set.remove(s[left])
            left += 1
        char_set.add(s[right])
        max_len = max(max_len, right - left + 1)

    return max_len

Approach 3: Optimized Sliding Window with HashMap

Algorithm:

1. Use a hash map to store the last index of each character.
2. Move the right pointer to expand the window.
3. If a duplicate character is found, update the left pointer to the position right after the last occurrence of the character.
4. Keep track of the maximum length of substrings found.

Time Complexity: (O(n))
Space Complexity: (O(min(n, m)))

Python Code:

def lengthOfLongestSubstring(s: str) -> int:
    n = len(s)
    char_index_map = {}
    left = 0
    max_len = 0

    for right in range(n):
        if s[right] in char_index_map:
            left = max(left, char_index_map[s[right]] + 1)
        char_index_map[s[right]] = right
        max_len = max(max_len, right - left + 1)

    return max_len

FAQ

Q1: What is the main idea behind the sliding window approach?

• The sliding window approach involves maintaining a window of characters without duplicates and adjusting the window size dynamically as we encounter duplicates.

Q2: Why is the brute force approach inefficient?

• The brute force approach checks all possible substrings, resulting in a time complexity of (O(n^3)), which is impractical for large strings.

Q3: How does the optimized sliding window with hash map improve performance?

• The optimized sliding window approach uses a hash map to keep track of the indices of characters, allowing us to skip over duplicates efficiently and maintain (O(n)) time complexity.

Q4: Can these algorithms handle strings with non-alphabetic characters?

• Yes, all the provided algorithms can handle strings with any type of characters, including digits, symbols, and spaces.

Q5: What is the space complexity of the sliding window approaches?

• The space complexity is (O(min(n, m))), where (n) is the length of the string and (m) is the size of the character set. This is because the sliding window uses a set or hash map to store characters.

By understanding these approaches and their complexities, you can efficiently solve the problem of finding the longest substring without repeating characters.